Guaranteed outlier removal for point cloud registration with correspondences
Guaranteed outlier removal for point cloud registration with correspondences
Abstract
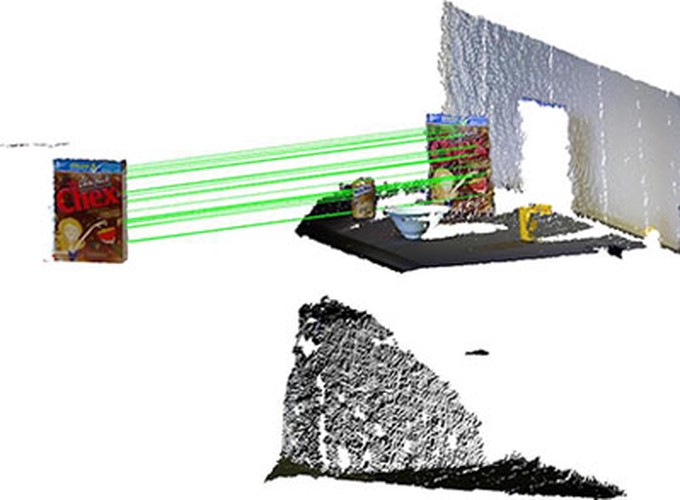
An established approach for 3D point cloud registration is to estimate the registration function from 3D keypoint correspondences. Typically, a robust technique is required to conduct the estimation, since there are false correspondences or outliers. Current 3D keypoint techniques are much less accurate than their 2D counterparts, thus they tend to produce extremely high outlier rates. A large number of putative correspondences must thus be extracted to ensure that sufficient good correspondences are available. Both factors (high outlier rates, large data sizes) however cause existing robust techniques to require very high computational cost. In this paper, we present a novel preprocessing method called guaranteed outlier removal for point cloud registration. Our method reduces the input to a smaller set, in a way that any rejected correspondence is guaranteed to not exist in the globally optimal solution. The reduction is performed using purely geometric operations which are deterministic and fast. Our method significantly reduces the population of outliers, such that further optimization can be performed quickly. Further, since only true outliers are removed, the globally optimal solution is preserved. On various synthetic and real data experiments, we demonstrate the effectiveness of our preprocessing method. Demo code is available as supplementary material.