Abstract

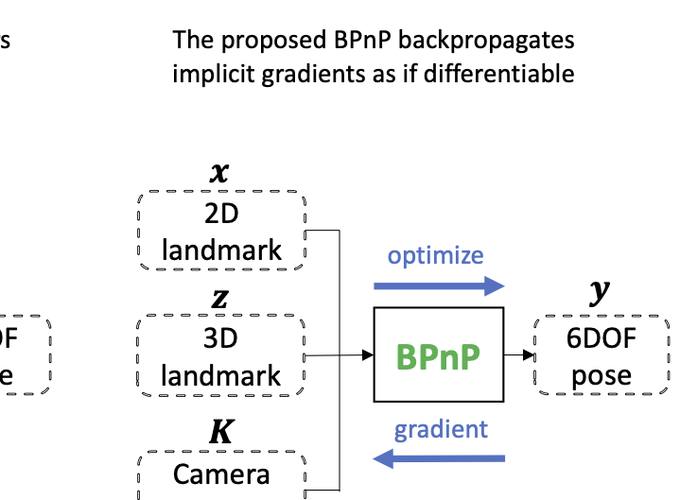
Deep networks excel in learning patterns from large amounts of data. On the other hand, many geometric vision tasks are specified as optimization problems. To seamlessly combine deep learning and geometric vision, it is vital to perform learning and geometric optimization end-to-end. Towards this aim, we present BPnP, a novel network layer that backpropagates gradients through a Perspective-n-Points (PnP) solver to guide parameter updates of a neural network. Based on implicit differentiation, we show that the gradients of a ‘self-contained’ PnP solver can be derived exactly and efficiently, as if the optimizer block were a differentiable layer. We validate BPnP by incorporating it in a deep model that can learn camera intrinsics, camera extrinsics (poses) and 3D structure from large datasets. Further, we develop an end-to-end trainable pipeline for object pose estimation, which achieves greater accuracy by combining feature-based heatmap losses with 2D-3D reprojection errors. Since our approach can be extended to other optimization problems, our work helps to pave the way to perform learnable geometric vision in a principled manner.