Further Enquiries

School of Computer and Mathematical Sciences
Ingkarni Wardli Building
The University of Adelaide
SA 5005
AUSTRALIA
Email

Telephone: +61 8 8313 5586
Facsimile: +61 8 8313 4366

Supplementary material for the article "Beyond the edge of feasibility: analysis of bottlenecks"

The following stories represent different industrial scenarios. They are based on personal experience and on examples from "Eiselt, Sandblom: Linear Programming and its applications, Springer, 2007". We provide several default values, however, all parameters can be changed to create new instances of the stories that possibly have different characteristics.

Job shop scheduling

There are n jobs, each has m operations. Each operation needs to be run in an uninterruptable process and the operations are run sequentially (their order is important). Also there are m machines that can handle these operations (operation ij can be handled by the machine M_ij). Each operation in a job is run in a different machine with different processing times (operation ij needs t_ij time units to be processed by the machine M_ij). Each machine can process only one operation at a time. The aim is to find the best order of running the operations for all jobs to minimize the makespan, the completion time of the last operation. See [1] for the MIP model.

Let us assume that the manufacturer can improve the performance of the machine k with the price l_k in a way that it can process each operation %f faster. However, this performance improvement cannot be over %max from the original setting. For different budgets, find the best investment (which machine should be tuned up) and the best schedule to minimize makespan.

Car manufacturing problem (continuous space)

A company manufactures n types of cars, each car type i contributes $c_i to the benefit. There are m machines, to manufacture a car type i, each machine j is utilized by t_ij (for a day). s_i tons of steel is needed to manufacture the car type i. Each day, the company can rent up to r_j machines type j at a cost of $d_j per machine. Also, there are only k tons is available per day. Marketing considerations dictate that at least l_i cars from the car type i be produced per day. The company is after the number of each type of cars to produce and number of machines to rent daily such that the total daily profit is maximized while constraints are not violated.

Decision variables:
- x_i is the number of cars from type i to produce (integer)
- M_j is the number of machines from the type j that should be rented (integer)

Objective function:
- $\max _{x,M} \left(\sum _{i=1}^{n}c_{i} x_{i} -\sum _{j=1}^{m}M_{j} d_{j} \right)$ is the objective function: benefit from total produced cars subtracted by the rented

Constraints:
- $\sum _{i=1}^{n}t_{j} x_{i} \le M_{j}$ for all : the total number of used machines of the type should be less than total number of rented from that type
- $\sum _{i=1}^{n}s_{i} x_{i} \le K$ : the total amount of the used steel per day should be less than
- $x_{i} \le l_{i}$ for all : marketing consideration
- $M_{j} \le r_{j}$ for all : the number of rented machines is limited

Let us assume that each machine can be tunned up with the price of $tune_i to reduce the duration for production by %reduce_i less than original (t_j) for manufacturing car type i. However, the minimum utilization to manufacture a car is %minu_i. Also, the maximum number of each machine that can be rented (r_j) is increased by 1 with the cost of $inc to the maximum of maxinc. Moreover, the available steel tonnages can be increased for $st per ton. The manufacturer is interested to find out what is the best way of investment for different amount of available budgets.

Traveling thief problem

There are

cities and

items have been distributed among these cities and the cities distances are given (distance between city

is given by

). A thief is going to travel around these cities, take a complete tour, visit each city exactly once, and get back to the starting city. Also, the thief is going to steal some items (each item

has the weight

and profit

) during the tour and put them in a knapsack (maximum weight that of the knapsack is

), however, carrying more items reduces the speed of the thief. The speed of the thief is a function of the weight he is carrying in his knapsack, that is given by:

$v_i=(v_{max}-W_i\frac{v_{max}-v_{min}}{W}))$

where is the weight of the knapsack when the thief is about to leave city . According to the speed of the thief, the travel time from the city to is calculated by:

$t_{ij}=\frac{d(i, j)}{v_i}$

Also, the thief has rented the knapsack and he has to pay for the rent as soon as he arrives back to the starting city. The rent rate for the knapsack is % per time unit. The thief is going to take the tour and collect items in a way that his profit is maximized. Assume that the tour is given by the permutation :

$\sum\limits_{i=1}^{n}(min(x_i,1)p_i)-R(\sum\limits_{i=1}^{m-1}(t_{P_iP_{i+1}})+t_{P_mP_1})$

where represents the city number where item is picked from, and it is zero if item is not picked at all.

The thief is also interested to know if he wants to invest on his , i.e. $v_{max}$ and $v_{min}$ and/or the size of his knapsack (), what would be the best way of this investment and what will be the corresponding objective value. $v_{max}$ can be increased by 1 unit by paying $ $vinc_{max}$ (floating points are allowed), $v_{min}$ can be increased by 1 unit by paying $ $vinc_{min}$ , and $v_{min} \le v_{max}$ . Also, can be increased by 1 unit (floating points are allowed) for $.

If you want to learn more about the Traveling Thief Problem, then have a look at the corresponding project page.

Agricultural allocation

Disclaimer: this example is taken from the above-mentioned Eiselt-Sandblom book, and our extension is the data on investments.

A farmer owns 1,000 acres of more or less homogeneous farmland. His options are to breed cattle, or plant wheat, corn, or tomatoes. It takes four acres to support one head of cattle. Annually, 12,000 hours of labor are available. (For simplicity, we will assume here that these 12,000 hours could be used at any time during the year, i.e., through hiring casual labor during seasons of high need, e.g., for harvesting).

In the following, we list information regarding the profit, yield, and labor needs for the four economic activities:
- cattle: $1,600 /head profit, 0.25 heads/acre yield, 40 h/head annual labor
- wheat: $5 /bushel profit, 50 bushels/acre yield, 10 h/acre annual labor
- corn: $6 /bushel profit, 80 bushels/acre yield, 12 h/acre annual labor
- tomatoes: 50 cent/lb profit, 1,000 lbs/acre yield, 25 h/acre annual labor

Furthermore, it is required that at least 20% of the farmland that is cultivated in the process must be used for the purpose of cattle breeding, at most 30% of the available farmland can be used for growing tomatoes, and the ratio between the amount of farmland assigned to growing wheat and that left uncultivated should not exceed 2 to 1.

Now (and this is our extension), the farmer can make certain investments that can possibly increase the overall profit per year:
- Additional acres of farmland can be rented for farm_rent=$200 per year. Up to 1000 (2000 in total) additional acres is allowed while no selling is allowed (minimum 1000 acres is available).
- Additional labor can be hired at labour_cost=$20 per hour. Up to 3000 additional hours are allowed (15000 in total) while no selling is allowed (minimum 12000 labor hours is available).
- A tomato packing machine can be rented for machine_cost=$5,000 per year, which reduces 25 h/acre to 20 h/acres.
- With a yearly investment of licence_tomato=$10,000 for a "tomato grower's licence", the max ratio of 30% can be increased to 35%.
- the value 0.25 heads/acre can be improved up to 0.7 heads/acres for $10,000 (0.25 needs 0$, 0.7 needs $10,000, and anything in between is linear).

The question is: should the farmer invest, and if so, how?
For your convenience: a linear programming formulation is available here.

Portfolio selection

Disclaimer: this example is taken from the above-mentioned Eiselt-Sandblom book, and our extension is the data on investments. An investor has $1 million to invest in any combination of bonds, stocks, term deposits, a savings account, real estate, and gold.

In the following, we list the anticipated (or known) interest rates, the risk factors (where a high number indicates a high risk) and the expected increase in the value of the investment:
- bonds: 5% interest annually, risk factor 3, 0% expected annual increase in value
- stocks: 2% interest, r.f. 10, 7% expected increase
- term deposits: 4% interest, r.f. 2, 0% expected increase
- savings account: 3% interest, r.f. 1, 0% expected increase
- real estate: 0, r.f. 5, 7% expected increase
- gold: 0, r.f. 20, 11% expected increase

For instance, real estate does not yield any interest (the projects are not rental properties), but its value is expected to increase by 7% per year. On the other hand, stocks yield an average of 2% in interest, and in addition to that, they are expected to increase in value by 7% for a total of 9% p.a. The other numbers are to be interpreted similarly.

The objective is to maximize the amount that is expected to be available in a year’s time subject to the following restrictions:
- Of the total amount of money invested, at least 30% must be invested in bonds, not more than 10% in stocks, and at least 10% in term deposits and/or savings accounts.
- Up to 50% of the total money invested in real estate may be borrowed against in the form of a mortgage at an interest rate of 6%. The amount borrowed cannot exceed $150,000.
- The average risk factor of the investment cannot exceed 4.5.
- The average annual interest should be at least 2.5%.
- The amount of money invested in gold cannot exceed $100,000 or 8% of the total amount of money available, whichever is smaller.

In this case, money is the only scarce resource. The investor now can make investments in order to increase the maximum possible profit:
- At loan_rate=3%, he can get a loan of loan_amount=$100,000 from a good friend.
- For gold_info=$1,000, he can get insider information on the development of gold that increases his expected increase for his gold investments by 2%
- He wonders if it is necessary to stick to his rule "average annual interest >=2.5%". At no cost, he might change his mind and discard this rule.

Mini mine-to-port supply chain

There is a mine company that has the following resources for the mine operations:

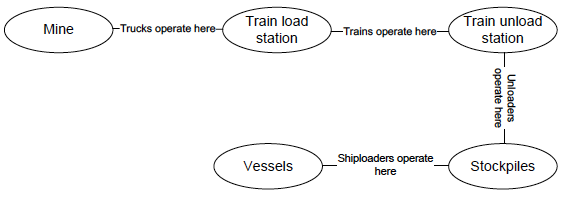
Trucks: n=100 trucks with capacity truckc_i=400 tons of product, they take products from the mine and load that into a train. It takes truckt₁=20 minutes to carry truckc_i tons to a train loading station and load to the train, and truckt₂=10 minutes to get back to the mine.

Trains: m=3 trains with capacity trainc_i=14,000 tons of product, they take products from the train load station and take that to the train unload station. It takes traint₁=180 minutes to carry trainc_i tons to a train unloading station, and traint₂=120 minutes to get back to the loading station.

Train unloader: u=3 train unloaders with the operation rate unloaderr_i=50 tones per minute (tpm). They unload products from trains and load then into the stockpiles.

Stockpiles: s=5 stockpiles in the port, with the capacity stockpilec_i=150,000 tones.

Ship loader: l=2 ship loaders with the operation rate loaderr_i=100 tones per minute. They take products from stockpiles and load then into the vessels (the assumption is there is always a vessel ready to be loaded).

The mine owner is after the best schedule for the trucks, trains, assignment of the trains to unloaders, unloader schedules, unloader assignments to stockpiles, and loader schedules for one month.

Also, the mine owner is interested in investment options as well:

Each truck costs $truckPrice=$5,000,000 (with the default capacity), tuning up of the trucks is possible in the following way: capacity of each truck is tuned up with the cost of $truckCap=$10,000 per ton, to the maximum of truckCapMax=500 tons.

Each train costs $trainPrice=$9,000,000 (with the default capacity), tuning up of the trains is possible in the following way: capacity of each train is tuned up with the cost of $trainCap=$120,000 per wagon (each wagon adds wagonTon=300 tons to the capacity) per train, up to trainCapMax=25,000 tons. Note that, usually mine owners do not own trains as train costs are very high. Thus, they normally rent trains and the given price is the rent price for one month of a train. Also, the mine owners book rails for the usages of their trains. However, here we have assumed that the rail is always available.

Each train unloader costs $unloaderPrice=$7,000,000 (with the default rate), tuning up of the unloaders is possible in the following way: rate of each unloader is tuned up with the cost of $unloaderRate=$15,000 per tpm, up to unloaderRateMax=80.

Adding one stockpile costs $stockpileAdd=$1,500,000, to the maximum of maxNumStockpile = 10

Each train loader costs $loaderPrice=$8,000,000 (with the default rate), tuning up of the trains is possible in the following way: rate of each loader is tuned up with the cost of $loaderRate=$14,000 per tpm, to the maximum of loaderRateMax = 150

What is the best way of investment for the mine owner for different budgets to maximize the transported tonnage in one month?

(click to enlarge)

Mine-to-port supply chain

There is a mine company that has the following resources for the mine operations:

Trucks: similar to the mini mine operation, but, each truck goes for maintenance after transporting truckm = 40,000 tons for trucktm = 600 minutes,

Trains: similar to the mini mine operation, but, each train goes for maintenance after transporting trainm=300,000 tons for traintm = 1800 minutes,

Train unloader: similar to the mini mine operation, but, each unloader goes for maintenance after unloaderm = 3,000,000 tons of activity for unloadertm = 1800 minutes

Stockpiles:similar to the mini mine operation

Ship loader: similar to the mini mine operation, but, each loader goes for maintenance after loaderm = 6,000,000 tons of activity for loadertm = 1,440 minutes

The mine owner is after the best schedule for the trucks, trains, assignment of the trains to unloaders, unloader schedules, unloader assignments to stockpiles, and loader schedules for one month.

Also, the mine owner is interested in investment options as well:

the costs for the resources are all similar to the one in the mini mine operation. For tune ups, there is one more option for each resource:

Trucks: maintenance time trucktm is reduced with the cost of truckmtunecost = $100 per truck per minutes, to the minimum of truckMinimumM = 300 minutes

Trains: maintenance time traintm is reduced by one minute with the cost of trainmtunecost = $200 per train per minutes to the minimum of trainMinimumM = 1200 minutes

Train unloader: maintenance time unloadertm is reduced with the cost of unloadermtunecost = $1500 per unloader per minutes to the minimum of unloaderMinimumM = 1200 minutes

Stockpiles: Adding stockpiles is possible (see minim mine operation)

Ship loader: maintenance time loadertm is reduced with the cost of loadermtunecost = $1500 per loader per minutes, to the minimum of loaderMinimumM = 1200 minutes

What is the best way of investment for the mine owner for different budgets to maximize the transported tonnage in one month